|
|
|
PermainanMemindahkan blok berbentuk lingkaran yang membentuk menara, memindahkan ke lokasi lain, namun blok lingkaran besar selalu harus berada dibawah blok lingkaran kecil. Dalam Gambar 1 disajikan animasi yang memindahkan menara dari kiri ke kanan, sesuai dengan aturan yang telah ditetapkan.  Gambar 1. Ilustrasi pemindahan Menara Hanoi (dari Wikipedia) Permainan ini menjadi sangat populer, karena mengajarkan beberapa keteraturan (algoritma) yang harus dicermati untuk memindahkan blok-blok tersebut. Walaupun algoritma tersebut hanya bisa dicerna oleh orang dewasa, namun demikian permainan ini sudah dikenalkan sejak dini kepada kanak-kanak. Gambar 2 dann 3, merupakan contoh permainan menara di atas yang terkenal dengan sebutan Menara Hanoi yang dibuat oleh pelbagai perusahaan mainan anak-anak.  Gambar 2. Mainan anak Menara Hanoi dari perusahaan Maya Organic
Peraturan PermainanPermainan ini terdiri dari tiga kolom dan beberapa blok dengan ukuran yang berbeda yang dapat diletakkan pada masing-masing kolom. Permainan ini dimulai dengan meletakkan blok ke dalam kolom dari yang terbesar pada bagian terbawah dan yang terkecil pada bagian yang teratas, sehingga berbentuk menara. Tujuan dari permainan ini adalah memindah seluruh menara dari kolom satu ke kolom yang lain; dengan memenuhi aturan sebagai berikut:
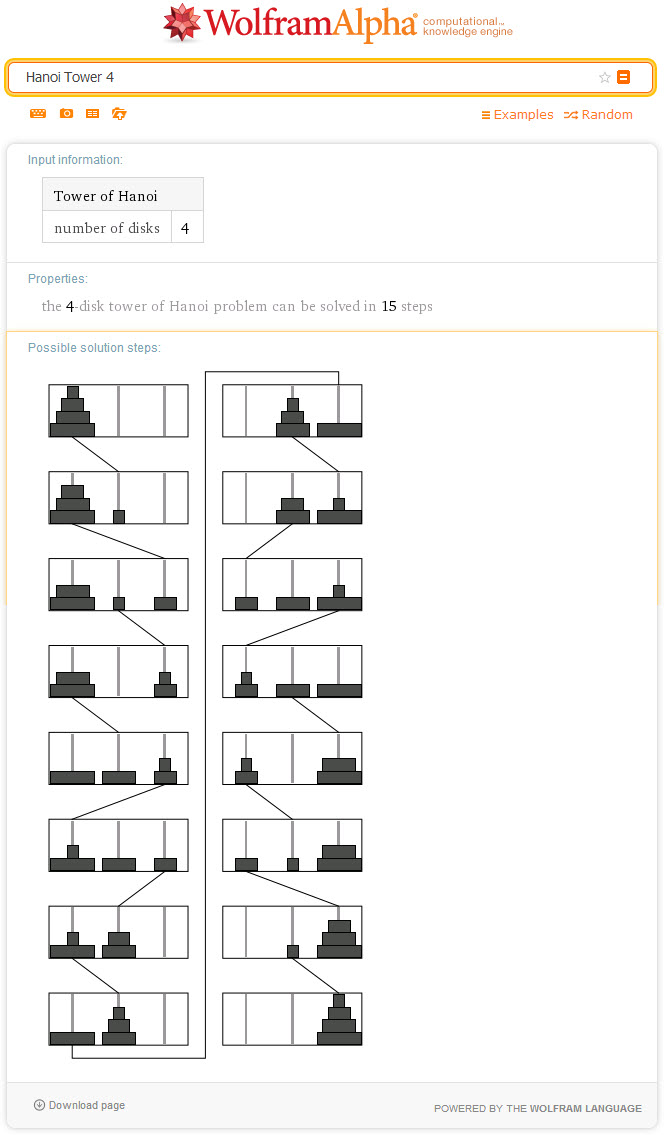
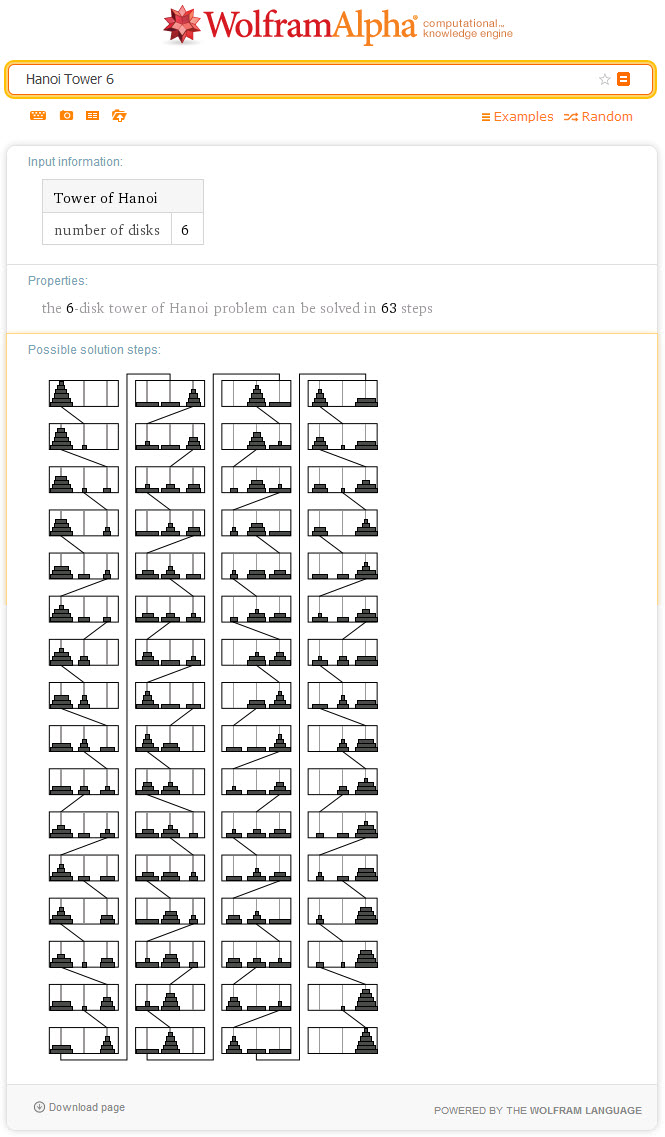
SejarahPermainan ini digagas oleh ahli matematika dari Perancis bernama Édouard Lucas pada tahun 1883. Pada saat menggagas permainan ini Lucas juga membarengi dengan sebuah kisah yang dapat dibaca pada Wikipedia. PenyelesaianPermainan ini dapat diselesaikan dalam 2n-1 langkah, dengan n adalah jumlah blok lingkaran. Jika terdapat 64 blok yang harus dipindahkan, maka dibutuhkan 264-1 atau 18.446.744.073.709.551.615 langkah. Jika setiap langkah membutuhkan waktu 1 detik, dibutuhkan sekitar 585 milyar tahun, setara dengan 127 kali usia matahari sekarang. Penyelesaian dengan bahasa pemrograman ada dua jenis yaitu (1) iteratif, dan (2) rekursif. Contoh penyelesaian dengan Wolfram Alpha untuk 3 kasus disajikan pada Gambar 4-6 di bawah ini. 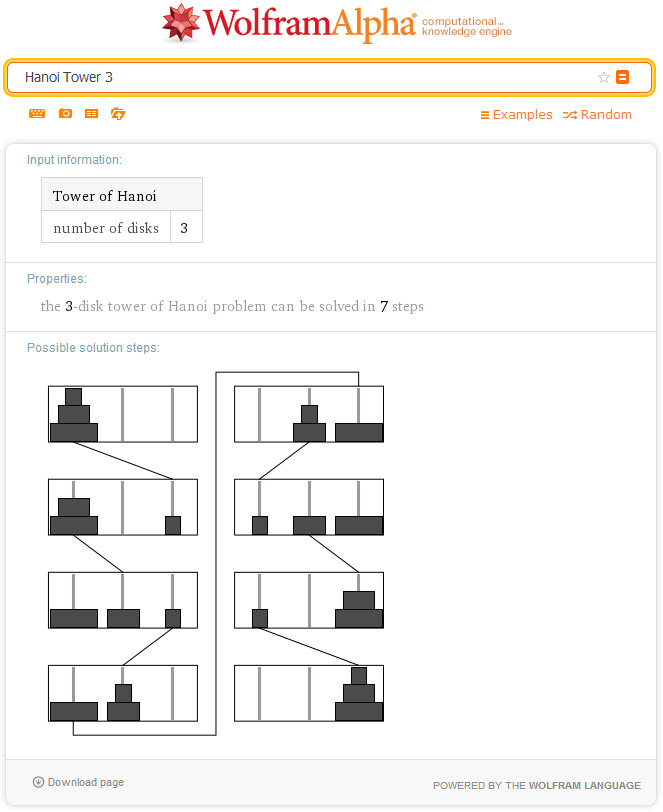 Gambar 4. Penyelesaian Menara Hanoi 3 blok dengan Wolfram Alpha.
TugasSetiap mahasiswa diharuskan mempelajari permainan Menara Hanoi dan menemukan keteraturan dalam langkah-langkah pemindahan blok lingkaran. Keteraturan langkah inilah yang didalam pemrograman komputer disebut dengan algoritma (langkah-langkah penyelesaian). Pelajari Gambar 4-6 dan video pada Daftar Pustaka untuk menemukan keteraturan tersebut. Algoritma ini kemudian disusun dalam bahasa pemrograman tertentu dan dapat dipelajari pada situs Rosetta. Pustaka
|
|
|
oleh Ir. Djoko Luknanto, M.Sc., Ph.D. (Djoko Luknanto, Jack la Motta, Luke Skywalker) (Alamat situs ini: http://luk.staff.ugm.ac.id/komputer/, http://luk.tsipil.ugm.ac.id/komputer/) Pensiunan Peneliti Sumberdaya Air |